
 |
Движение заряженных частицводнородном магнитном полеРассмотрим частный случай, когда нет электрического поля, но имеется магнитное поле. Предположим, что частица, обладающая начальной скоростью u0, попадает в магнитное поле с индукцией B. Это поле мы будем считать однородным и направленным перпендикулярно к скорости u0.
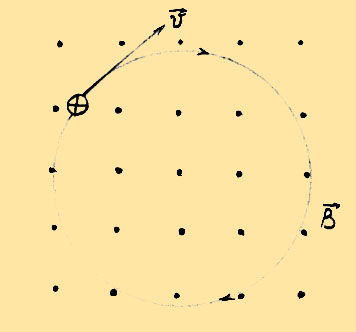 Основные особенности движения в этом случае можно выяснить, не прибегал к полному решению уравнений движения. Прежде всего, отметим, что действующая на частицу сила Лоренца всегда перпендикулярна к скорости движения частицы. Это значит, что работа силы Лоренца всегда равна нулю; следовательно, абсолютное значение скорости движения частицы, а значит, и энергия частицы остаются постоянными при движении. Так как скорость частицы u не изменяется, то величина силы Лоренца остается постоянной. Эта сила, будучи перпендикулярной, к направлению движения, является центростремительной силой. Но движение под действием постоянной по величине центростремительной силы есть движение по окружности. Радиус r этой окружности определяется условием 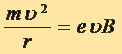
откуда 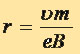
Если энергия электрона выражена в эВ и равна U, то 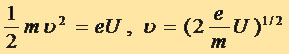 (3.6) (3.6)
и поэтому 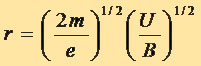
Кругообразное движение заряженных частиц в магнитном поле обладает важной особенностью: время полного обращения частицы по окружности (период движения) не зависит от энергии частицы. Действительно, период обращения равен 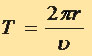
Подставляя сюда вместо r его выражение по формуле (3.6), имеем: 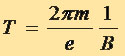 (3.7) (3.7)
Частота же оказывается равной 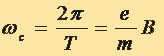
Для данного типа частиц и период, и частота зависят только от индукции магнитного поля. Выше мы предполагали, что направление начальной скорости перпендикулярно к
направлению магнитного поля. Нетрудно сообразить, какой характер будет
иметь движение, если начальная скорость частицы составляет некоторый угол
с направлением поля. В результате сложения обоих движений частица будет двигаться по цилиндрической спирали. Шаг винта этой спирали равен подставляя вместо T его выражение (3.7), имеем: 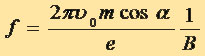
|